问题描述
在数据挖掘,或者普通数据筛选业务中,我们常常会遇到以下类似的问题:
例如:
我们有学生数据表,包含了学生的数据字段有[性别,年龄,身高,体重,血型],现在有需要在未知数据量(可能很多,可能很少)的数据池中筛选出90条数据,保证这90条数据满足以下条件:
- 男女比例各一半,也就是男生45条数据,女生45条数据
- 只需要身高在7米以下的学生
- 只需要年龄在15到20岁之间
- 学生体重在100斤以下的需要60个,100斤以上的需要30个
- 学生血型是A型血的需要 36个,是B型血的需要54个
我们可以看出,这些条件大部分都是相互交叉的,也就是说有些学生可能满足多条限制条件,因此简单的按照条件用数据库查询是很难办到的。其中的难点就在于,更改某个条件的学生人数的时候,这些学生很可能也满足其他条件,这样就会打破其他条件的平衡。
这里我们使用的方法是:相互控制配额抽样模型
模型介绍
相互控制配额抽样又称“非独立控制配额抽样”,是指在按各类控制特性独立分配样本数额基础上,再采用交叉控制安排样本的具体数额的抽样方式。
具体方法
回到我们的例子,我们要完成目标条件,需要做以下几步
第一步:确定边界
数据库里面的数据,可能包含了我们并不需要的数据,所以我们在第一步需要做第一层筛选,把完全不满足的数据过滤掉,这就叫确定数据边界。
比如
- 只需要身高在7米以下的学生(我们需要把身高在1.8米以上的学生过滤掉)
- 只需要年龄在15到20岁之间(我们需要把15岁以下,20岁以上的学生过滤掉)
- 学生血型是A型血的需要 36个,是B型血的需要54个(我们需要把其他血型的学生过滤掉)
这样我们的基础数据样本池就确定了
第二步:确定分层和比重
我们从满足的条件可以看出,有数据比例限制的只有3条:
- 男女比例各一半,也就是男生45条数据,女生45条数据
- 学生体重在100斤以下的需要60个,100斤以上的需要30个
- 学生血型是A型血的需要 36个,是B型血的需要54个
所以,在这个模型中,我们需要设定3层抽样(过滤)条件,以及比重
第一层:男1/2(45),女1/2(45)
第二层:<=100斤2/3(60),>100斤1/3(30)
第三层:A型2/5(36),B型3/5(54)
第三步:相互控制配额样本表
根据每层的占比,按照同样的占比一层一层划分下去,最终会形成这样的一张配额表
|
(总数) 90 |
|||||||
|
(男) 45 |
(女) 45 |
||||||
|
(<=100斤) 30 |
(>100斤) 15 |
(<=100斤) 30 |
(>100斤) 15 |
||||
|
(A型) 12 |
(B型) 18 |
(A型) 6 |
(B型) 9 |
(A型) 12 |
(B型) 18 |
(A型) 6 |
(B型) 9 |
可以看出,我们需要从数据库这样筛选出数据:
- 小于100斤A型血的男生,12名
- 小于100斤B型血的男生,18名
- 大于100斤A型血的男生,6名
- 大于100斤B型血的男生,9名
- 小于100斤A型血的女生,12名
- 小于100斤B型血的女生,18名
- 大于100斤A型血的女生,6名
- 大于100斤B型血的女生,9名
这样就能满足所有条件:
- 男女比例各一半,也就是男生45条数据,女生45条数据
- 学生体重在100斤以下的需要60个,100斤以上的需要30个
- 学生血型是A型血的需要 36个,是B型血的需要54个
第四步:二叉树动态规划
这样预先设定了需要筛选的条件的目标数量,但是还这样的问题:
比如:
- 数据库小于100斤A型血的男生,根本不足12名呢?
- 或者因为特殊业务需求小于100斤A型血的男生,我们需要最少13名呢?
从我们第三步的相互控制配额样本表给出的结果,我们可以把它称为理想值,或者最优解,但是并不代表这是唯一的结果,我们只需要动态调整数据,就能在不破坏整体条件的基础上,获得其他结果。
这里用到的是二叉树最小影响理论,我们可以把所有的分层想象成一颗二叉树:
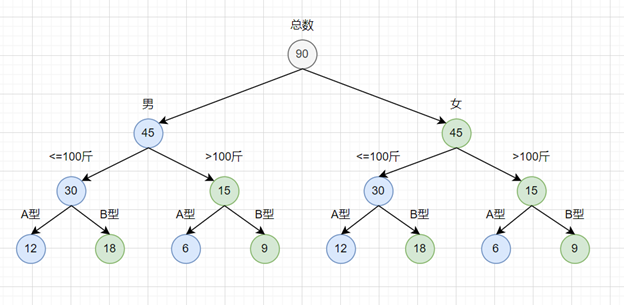
二叉树的子节点都有两个属性,我们标记为蓝色和绿色
这样可以看出,每一层颜色的总和是满足一个条件的。
比如:
- 第二层蓝色之和是男生45,绿色之和是女生45
- 第三层蓝色之和是<=100斤为60,绿色之和是>100斤为30
- 第四层蓝色之和是A型血36,绿色之和是B型血54
所以想要要调整数额,就要保证颜色之和不变,而所谓最小单元理论是从二叉树最底层开始调整,这样就不会把影响扩散到父级。
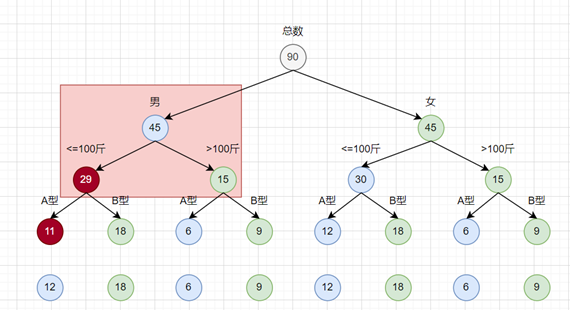
比如,如果A型血,<=100斤,男生只有11名
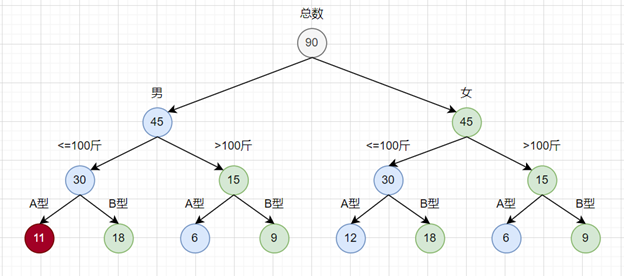
那么它所在的最小单元二叉树需要调整满足2个条件即可:
- 所在当前节点总和不变,所以同辈节点(也就是B型)需要调整
因为A型少了1个,所以B型加一个即可
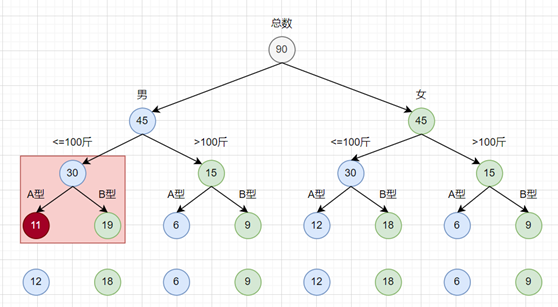
- 所在属性节点(蓝色)总和不变,所以找邻近的一个蓝色调整即可
但邻近的蓝色节点,也必须满足条件1,所以最终调整如下
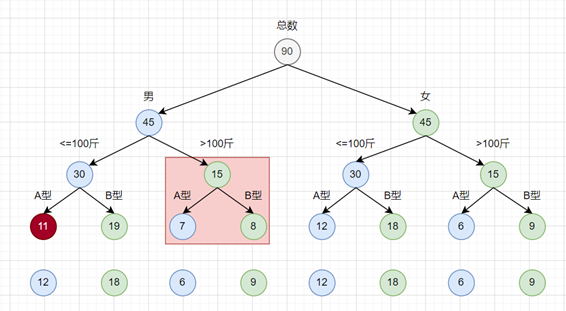
这样我们就完成了最小单元化的二叉树动态规划。
然而新的问题也随之而来了,如果出现某个节点在变化数据之后,小于0了,或者大于数据库最大上限值了怎么办?
我们可以用同样的理论,重新规划,只不过需要扩散最小单元的范围,把最小单元扩散至更上一层。我们忽略这一层,再更上一层去做同样的调整。
那么我们得到的调整数据将会出现在父节点的值上,这时候,我们只需要在同属性节点(比如这里少一个的是蓝色)的所有子节点上调整即可。
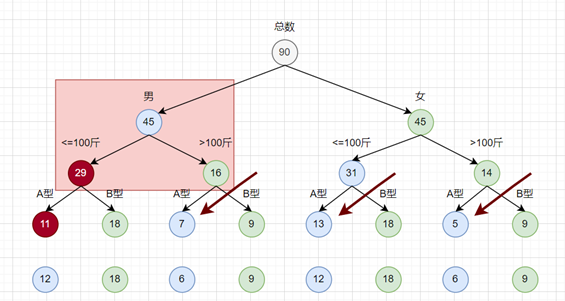
如果还是没有合适的结果,那继续往父类扩散即可,直到无法扩散,那就找不到合理的结果。
第五步:从数据库筛选数据
这里就涉及到数据分布的问题,要随机查询,还是想顺序查询,还是想均匀分布,动态分布?这就和业务需求挂钩了,不在本模型的讨论范围。
总结
我们可以看出,利用这个模型,我们可以解决很多交叉条件,这些条件又相互制约的比例筛选数据场景。其中包含了数学模型和数据机构模型,统计学等相关知识。不理解的地方可以多多加深这方便的知识。
代码:
先看测试类:
public class FoldSamplingBuilderTest {
@Test
public void samplingCaseOne() {
//given
Condition male = Condition.of("male", 45);
Condition female = Condition.of("female", 45);
Condition less100 = Condition.of("less100", 60);
Condition more100 = Condition.of("more100", 30);
Condition A = Condition.of("A", 36);
Condition B = Condition.of("B", 54);
int targetSamplesCount = 90;
//when
SamplingResultCollection result = FoldSamplingBuilder.newFoldSampling()
.targetSamplesCount(targetSamplesCount)
.addMutualExclusionCondition(less100, more100)
.addMutualExclusionCondition(male, female)
.addMutualExclusionCondition(A, B)
.addConditionSamplesLimitation(
ConditionLimitation.withLimit()
.and(male)
.and(less100)
.and(A)
.range(11, 50)
)
.addConditionSamplesLimitation(
ConditionLimitation.withLimit()
.and(female)
.and(less100)
.and(A)
.range(1, 50)
)
.sampling();
//then
result.print();
}
}
vo
public class Condition {
private String name;
private int count;
private ConditionType type = ConditionType.MUTUAL_EXCLUSION;
/**
* We not allow new Condition, please use static method {@link #of(String, int)} instead
*/
private Condition(String name, int count) {
this.name = name;
this.count = count;
}
/**
* We not allow new Condition, please use static method {@link #of(String, int, ConditionType)} ()} instead
*/
private Condition(String name, int count, ConditionType type) {
this.name = name;
this.count = count;
this.type = type;
}
/**
* Create new Condition
* @param name condition name
* @param count condition limit count
* @return Condition instance
*/
public static Condition of(String name, int count) {
return new Condition(name, count);
}
/**
* Create new Condition
* @param name condition name
* @param count condition limit count
* @param type condition type default is MUTUAL_EXCLUSION
* @see ConditionType#MUTUAL_EXCLUSION
* @return Condition instance
*/
public static Condition of(String name, int count, ConditionType type) {
return new Condition(name, count, type);
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public int getCount() {
return count;
}
public void setCount(int count) {
this.count = count;
}
public ConditionType getType() {
return type;
}
public void setType(ConditionType type) {
this.type = type;
}
public enum ConditionType {
MUTUAL_EXCLUSION
}
}
public class ConditionLimitation {
private List<Condition> conditions;
private int minimumCount;
private int maximumCount;
public int getMaximumCount() {
return maximumCount;
}
public void setMaximumCount(int maximumCount) {
this.maximumCount = maximumCount;
}
/**
* We not allow new ConditionLimitation, please use static method {@link #withLimit()} instead
*/
private ConditionLimitation(List<Condition> conditions, int minimumCount) {
this.conditions = conditions;
this.minimumCount = minimumCount;
}
/**
* Create new ConditionLimitation with builder approach
* @return ConditionLimitation instance
*/
public static ConditionLimitation withLimit() {
return new ConditionLimitation(new LinkedList<>(), -1);
}
/**
* Add more condition limitation
* @param condition condition which already set in SamplingBuilder
* @see FoldSamplingBuilder
* @return ConditionLimitation instance
*/
public ConditionLimitation and(Condition condition) {
this.conditions.add(condition);
return this;
}
/**
* Add range limitation
* @param maximumCount if only give maximum count, the minimum count default is 0
* @return ConditionLimitation instance
*/
public ConditionLimitation range(int maximumCount) {
this.maximumCount = maximumCount;
return this;
}
/**
* Add range limitation
* @param minimumCount minimum count for this condition
* @param maximumCount maximum count for this condition
* @return ConditionLimitation instance
*/
public ConditionLimitation range(int minimumCount, int maximumCount) {
this.minimumCount = minimumCount;
this.maximumCount = maximumCount;
return this;
}
public List<Condition> getConditions() {
return conditions;
}
public void setConditions(List<Condition> conditions) {
this.conditions = conditions;
}
public int getMinimumCount() {
return minimumCount;
}
public void setMinimumCount(int minimumCount) {
this.minimumCount = minimumCount;
}
}
public class SamplingResultCollection {
private final List<String> headers;
private final List<List<Integer>> collections;
private Map<String, Integer> optimalSolution;
private Map<String, Integer> balancedSolution;
private final Map<String, Integer> conditionRateMap;
public SamplingResultCollection(List<String> headers, List<List<Integer>> collections, Map<String, Integer> conditionRateMap) {
this.headers = headers;
this.collections = collections;
this.conditionRateMap = conditionRateMap;
}
/**
* Get the optimal solution
* @return optimal solution, key is the condition name chain, value is the target sample count
*/
public Map<String, Integer> getOptimalSolution() {
if (optimalSolution == null) {
calculateOptimalSolution();
}
return optimalSolution;
}
/**
* If give condition limitation and need balance solution
* This will get the balanced solution
* If not give condition limitation this will give optimal solution
* @return balanced solution, key is the condition name chain, value is the target sample count
*/
public Map<String, Integer> getBalancedSolution() {
return balancedSolution == null ? getOptimalSolution() : balancedSolution;
}
private void calculateOptimalSolution() {
optimalSolution = new LinkedHashMap<>();
List<Integer> _optimalSolution = collections.get(0);
BinaryOperator<String> strReduceFunc = (pre, next) -> {
if (pre.equals("")) {
return next;
} else {
return pre + SEPARATOR + next;
}
};
for (int i = 0; i < headers.size(); i++) {
String[] keyArray = headers.get(i).split("\\+");
String sortedKey = Arrays.stream(keyArray).sorted(Comparator.comparingInt(conditionRateMap::get)).reduce("", strReduceFunc);
optimalSolution.put(sortedKey, _optimalSolution.get(i));
}
}
public List<String> getHeaders() {
return headers;
}
public List<List<Integer>> getCollections() {
return collections;
}
public void setBalancedSolution(Map<String, Integer> balancedSolution) {
this.balancedSolution = balancedSolution;
}
// Just for testing, please delete this on PROD
public void print() {
System.out.println(headers.toString());
System.out.println(getBalancedSolution().values());
}
}
public class TreeNode {
private String name;
private int value;
private int initialValue;
private TreeNode parent;
private TreeNode leftChild;
private TreeNode rightChild;
private int level;
private boolean isLeft;
public void resetAllTreeValue(boolean rollback) {
for (TreeNode treeNode : getAllBottomChildTreeNodes()) {
treeNode.resetValue(rollback);
}
}
public String getNameChain() {
if (isTop()) {
return name;
} else {
return name + SEPARATOR + getParent().getNameChain();
}
}
public TreeNode getTop() {
if (isTop()) {
return this;
} else {
return getParent().getTop();
}
}
public void addValue(int value) {
if (isBottom()) {
this.value += value;
} else {
if (isLeft) {
getLeftChild().addValue(value);
} else {
getRightChild().addValue(value);
}
}
}
public void minusValue(int value) {
this.addValue(-value);
}
public boolean isLeft() {
return isLeft;
}
public void setLeft(boolean left) {
isLeft = left;
}
public TreeNode getPeerNode() {
if (isLeft) {
return getParent().getRightChild();
} else {
return getParent().getLeftChild();
}
}
public List<TreeNode> getAllBottomChildTreeNodes() {
if (isBottom()) {
List<TreeNode> result = new LinkedList<>();
result.add(this);
return result;
} else {
List<TreeNode> result = leftChild.getAllBottomChildTreeNodes();
result.addAll(rightChild.getAllBottomChildTreeNodes());
return result;
}
}
public int getLevel() {
return level;
}
public void setLevel(int level) {
this.level = level;
}
public TreeNode(String name) {
this.name = name;
}
public TreeNode(String name, int value) {
this.name = name;
this.value = value;
}
public boolean isTop() {
return parent == null;
}
public boolean isBottom() {
return leftChild == null && rightChild == null;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public int getValue() {
return value;
}
public void setInitialValue(int value) {
this.value = value;
this.initialValue = value;
}
private void resetValue(boolean rollback) {
if (rollback) {
this.value = this.initialValue;
} else {
this.initialValue = this.value;
}
}
public TreeNode getParent() {
return parent;
}
public void setParent(TreeNode parent) {
this.parent = parent;
}
public TreeNode getLeftChild() {
return leftChild;
}
public void setLeftChild(TreeNode leftChild) {
this.leftChild = leftChild;
}
public TreeNode getRightChild() {
return rightChild;
}
public void setRightChild(TreeNode rightChild) {
this.rightChild = rightChild;
}
public int getTreeMinValue() {
return getAllBottomChildTreeNodes().stream().map(TreeNode::getValue).min((pre, next) -> {
if (pre < next) {
return pre;
} else {
return next;
}
}).orElse(0);
}
}
核心方法
public final class FoldSamplingBuilder {
/**
* We not allow new builder, please use static method {@link #newFoldSampling()} instead
*/
private FoldSamplingBuilder() {
}
/**
* new FoldSampling instance
*
* @return FoldSampling instance
*/
public static FoldSampling newFoldSampling() {
return new FoldSampling();
}
public static class FoldSampling {
private int totalSampleCount = -1;
private int foldCount = 0;
private final List<Condition[]> conditions = new LinkedList<>();
private final List<ConditionLimitation> conditionLimitations = new LinkedList<>();
private final Map<String, Integer[]> usedLimitations = new HashMap<>();
private SamplingResultCollection result;
public static final String SEPARATOR = "+";
private String balancedKey;
private int balancedValue;
private final Map<String, Integer> conditionRateMap = new HashMap<>();
private final BinaryOperator<String> strReduceFunc = (pre, next) -> {
if (pre.equals("")) {
return next;
} else {
return pre + SEPARATOR + next;
}
};
private static final String ROOT = "Root";
/**
* We not allow new FoldSampling, please use builder {@link FoldSamplingBuilder} instead
*/
private FoldSampling() {
}
/**
* Set target samples count, this is limit the total count of sampling result
*
* @param total result sampling count
* @return this {@link FoldSampling} instance
*/
public FoldSampling targetSamplesCount(int total) {
this.totalSampleCount = total;
return this;
}
/**
* Add the mutual exclusion condition, you can add more conditions by multiple call
* this method
*
* @param conditionA mutual exclusion condition one, see {@link Condition}
* @param conditionB mutual exclusion condition another one, see {@link Condition}
* @return this {@link FoldSampling} instance
*/
public FoldSampling addMutualExclusionCondition(Condition conditionA, Condition conditionB) {
makeSureSetTargetSamplesCount();
validRate(conditionA, conditionB);
foldCount += 1;
this.conditions.add(new Condition[]{
conditionA, conditionB
});
int size = conditionRateMap.size() + 1;
conditionRateMap.put(conditionA.getName(), 10 * size);
conditionRateMap.put(conditionB.getName(), 10 * size + 1);
return this;
}
/**
* Do the sampling method, it will get the sampling result
*
* @return sampling result {@link SamplingResultCollection}
*/
public SamplingResultCollection sampling() {
makeSureSetTargetSamplesCount();
makeSureAddConditions();
result = new SamplingResultCollection(
new ArrayList<>(),
new ArrayList<>(),
conditionRateMap
);
contactConditionName("", 0);
if (foldCount == 1) {
int conditionACount = conditions.get(0)[0].getCount();
result.getCollections().add(List.of(conditionACount, totalSampleCount - conditionACount));
} else {
Map<Integer, List<Integer>> foldValueMap = new HashMap<>();
foldValueMap.put(0, List.of(totalSampleCount));
for (int i = 1; i <= foldCount; i++) {
List<Integer> foldValue = new ArrayList<>((int) Math.pow(2, i));
Condition[] foldCondition = conditions.get(i - 1);
List<Integer> parentFoldValue = foldValueMap.get(i - 1);
parentFoldValue.forEach(value -> {
int _value = (value * foldCondition[0].getCount()) / totalSampleCount;
foldValue.add(_value);
foldValue.add(value - _value);
});
foldValueMap.put(i, foldValue);
}
result.getCollections().add(foldValueMap.get(foldCount));
}
validConditionLimitation();
return result;
}
private void validConditionLimitation() {
if (CollectionUtils.isEmpty(conditionLimitations)) {
return;
}
Map<String, Integer[]> limitation = conditionLimitations.stream().map(conditionLimitation -> {
String key = conditionLimitation.getConditions().stream()
.map(Condition::getName).reduce("", strReduceFunc);
return Map.of(sortKey(key), new Integer[]{
conditionLimitation.getMinimumCount(),
conditionLimitation.getMaximumCount()
});
}).reduce(new HashMap<>(), (pre, next) -> {
pre.putAll(next);
return pre;
});
go(limitation);
}
private void go(Map<String, Integer[]> limitation) {
if (needBalance(result.getBalancedSolution(), limitation)) {
findBalancedResult(limitation);
}
}
private void findBalancedResult(Map<String, Integer[]> limitation) {
Map<String, Integer> solution = result.getBalancedSolution();
TreeNode treeNode = samplingSolutionToTree(solution);
// solution: 邻节点更改后,更改 父节点 的兄弟节点 的 子节点
boolean success = true;
List<TreeNode> bottomNodes = treeNode.getAllBottomChildTreeNodes();
for (TreeNode bottomNode : bottomNodes) {
if (isNeedBalancedBottomNode(bottomNode)) {
success = balanceNodeValue(bottomNode);
if (success) {
break;
}
}
}
if (!success) {
throw new SamplingException("There's no solution for given condition limit!");
}
solution = treeToSamplingSolution(treeNode);
result.setBalancedSolution(solution);
treeNode.resetAllTreeValue(false);
if (limitation.containsKey(balancedKey)) {
Integer[] value = limitation.remove(balancedKey);
usedLimitations.put(balancedKey, value);
}
go(limitation);
}
private boolean isNeedBalancedBottomNode(TreeNode treeNode) {
return balancedKey.equals(sortKey(treeNode.getNameChain(), true));
}
private boolean balanceNodeValue(TreeNode treeNode) {
treeNode.addValue(balancedValue);
treeNode.getPeerNode().minusValue(balancedValue);
TreeNode parentPeerNode = treeNode.getParent().getPeerNode();
if (treeNode.isLeft()) {
parentPeerNode.getLeftChild().minusValue(balancedValue);
parentPeerNode.getRightChild().addValue(balancedValue);
} else {
parentPeerNode.getRightChild().minusValue(balancedValue);
parentPeerNode.getLeftChild().addValue(balancedValue);
}
if (treeNode.getTreeMinValue() < 0
|| breakPreviousLimitation(
treeToSamplingSolution(treeNode))) {
if (treeNode.getLevel() == 2) {
return false;
} else {
treeNode.resetAllTreeValue(true);
return balanceNodeValue(treeNode.getParent());
}
}
return true;
}
private boolean breakPreviousLimitation(Map<String, Integer> solution) {
return needBalance(solution, usedLimitations);
}
private Map<String, Integer> treeToSamplingSolution(TreeNode treeNode) {
TreeNode top = treeNode.getTop();
List<TreeNode> bottomNodes = top.getAllBottomChildTreeNodes();
Map<String, Integer> result = new LinkedHashMap<>();
bottomNodes.forEach(node ->
result.put(sortKey(node.getNameChain(), true), node.getValue()));
return result;
}
private TreeNode samplingSolutionToTree(Map<String, Integer> solution) {
Map<String, TreeNode> treeNodeMap = new HashMap<>();
for (Map.Entry<String, Integer> box : solution.entrySet()) {
String[] boxKeys = box.getKey().split("\\+");
int value = box.getValue();
for (int i = 0; i < boxKeys.length; i++) {
StringBuilder treeNodeMapKey = new StringBuilder(boxKeys[0]);
for (int j = 1; j <= i; j++) {
treeNodeMapKey.append(SEPARATOR).append(boxKeys[j]);
}
if (!treeNodeMap.containsKey(treeNodeMapKey.toString())) {
TreeNode treeNode = new TreeNode(boxKeys[i]);
treeNode.setLevel(i + 1);
if (i != 0) {
StringBuilder parentTreeNodeMapKey = new StringBuilder(boxKeys[0]);
for (int j = 1; j < i; j++) {
parentTreeNodeMapKey.append(SEPARATOR).append(boxKeys[j]);
}
TreeNode parent = treeNodeMap.get(parentTreeNodeMapKey.toString());
treeNode.setParent(parent);
treeNode.setLevel(i + 1);
if (i + 1 == boxKeys.length) {
treeNode.setInitialValue(value);
}
if (parent.getLeftChild() == null) {
treeNode.setLeft(true);
parent.setLeftChild(treeNode);
} else if (parent.getRightChild() == null) {
parent.setRightChild(treeNode);
}
}
treeNodeMap.put(treeNodeMapKey.toString(), treeNode);
}
}
}
TreeNode top = new TreeNode(ROOT);
top.setLevel(0);
for (Map.Entry<String, TreeNode> node : treeNodeMap.entrySet()) {
String name = node.getKey();
TreeNode _node = node.getValue();
if (!name.contains(SEPARATOR)) {
_node.setParent(top);
if (top.getLeftChild() == null) {
_node.setLeft(true);
top.setLeftChild(_node);
} else {
top.setRightChild(_node);
}
}
}
return top;
}
private boolean needBalance(Map<String, Integer> solution, Map<String, Integer[]> limitation) {
if (foldCount == 1) {
throw new SamplingException("Can't adjust solution if there's only 1 condition fold!");
}
for (Map.Entry<String, Integer[]> next : limitation.entrySet()) {
String key = next.getKey();
if (!solution.containsKey(key)) {
throw new SamplingException("Condition limitation doesn't match existing condition, Please check added conditions!");
}
int minimum = next.getValue()[0];
int maximum = next.getValue()[1];
int solutionValue = solution.get(key);
if (solutionValue < minimum || solutionValue > maximum) {
balancedKey = key;
if (solutionValue < minimum) {
balancedValue = minimum - solutionValue;// +
} else {
balancedValue = maximum - solutionValue;// -
}
return true;
}
}
return false;
}
private void contactConditionName(String parentConditionName,
int conditionIndex) {
Condition[] condition = conditions.get(conditionIndex);
String conditionAName = "".equals(parentConditionName) ? condition[0].getName() : parentConditionName + SEPARATOR + condition[0].getName();
String conditionBName = "".equals(parentConditionName) ? condition[1].getName() : parentConditionName + SEPARATOR + condition[1].getName();
int nextConditionIndex = conditionIndex + 1;
if (nextConditionIndex < conditions.size()) {
contactConditionName(conditionAName, nextConditionIndex);
contactConditionName(conditionBName, nextConditionIndex);
} else {
result.getHeaders().add(conditionAName);
result.getHeaders().add(conditionBName);
}
}
private void makeSureAddConditions() {
if (this.foldCount == 0) {
throw new SamplingException("Please add conditions first!");
}
}
private void makeSureSetTargetSamplesCount() {
if (this.totalSampleCount <= 0) {
throw new SamplingException("Please input a valid target samples count first!");
}
}
private void validRate(Condition conditionA, Condition conditionB) {
if (conditionA.getCount() < 0 || conditionB.getCount() < 0) {
throw new SamplingException("Please input valid condition count!");
}
if (conditionA.getCount() + conditionB.getCount() != totalSampleCount) {
throw new SamplingException("Given condition count doesn't match target samples count!");
}
}
private String sortKey(String key) {
String[] keyArray = key.split("\\+");
try {
return Arrays.stream(keyArray).sorted(Comparator.comparingInt(conditionRateMap::get)).reduce("", strReduceFunc);
} catch (NullPointerException e) {
throw new SamplingException("Condition limitation doesn't match fold condition!");
}
}
private String sortKey(String key, boolean noRoot) {
if (!noRoot) {
return sortKey(key);
}
String[] keyArray = key.split("\\+");
try {
return Arrays.stream(keyArray).filter(name -> !name.equals(ROOT)).sorted(Comparator.comparingInt(conditionRateMap::get)).reduce("", strReduceFunc);
} catch (NullPointerException e) {
throw new SamplingException("Condition limitation doesn't match fold condition!");
}
}
/**
* Add condition limitation, you can multiple call this method add more condition limitations
*
* @param conditionLimitation see {@link ConditionLimitation}
* @return this {@link FoldSampling} instance
*/
public FoldSampling addConditionSamplesLimitation(ConditionLimitation conditionLimitation) {
conditionLimitations.add(conditionLimitation);
return this;
}
/**
* Add condition limitation
*
* @param conditionLimitations a condition limitation collection see {@link ConditionLimitation}
* @return this {@link FoldSampling} instance
*/
public FoldSampling addConditionSamplesLimitation(List<ConditionLimitation> conditionLimitations) {
this.conditionLimitations.addAll(conditionLimitations);
return this;
}
}
}